Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- Get
- java
- 테코테코
- redux-toolkit
- 항해99
- 알고리즘
- Algorithm
- 매일메일
- sw expert academy
- programmers
- useDispatch
- react-redux
- 항해플러스
- 코딩테스트합격자되기
- redux
- 리액트
- SW
- 이코테
- maeil-mail
- 프로그래머스
- 자바
- react-router
- json-server
- axios
- redux-saga
- JavaScript
- Python
- react
- createSlice
- C++
Archives
- Today
- Total
Binary Journey
[Algorithm] Dijkstra Algorithm (데이크스트라 알고리즘) 본문
Algorithm/알고리즘 스터디(2021.07)
[Algorithm] Dijkstra Algorithm (데이크스트라 알고리즘)
binaryJournalist 2021. 10. 5. 00:16반응형
알고리즘의 개요와 실습 환경 구축 - 인프런 | 학습 페이지
지식을 나누면 반드시 나에게 돌아옵니다. 인프런을 통해 나의 지식에 가치를 부여하세요....
www.inflearn.com
인프런 25강에 대한 리뷰다.
데이크스트라 알고리즘은 dp (dynamic programming)을 이용한 최단 경로 탐색 알고리즘이다.
그리드 알고리즘으로 분류되기도 한다.
(매번 가장 적은 비용의 노드를 선택해서 정렬하기 때문)
* 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다는 특징이 있다.
=> 현재까지 알고 있던 최단 경로를 계속해서 갱신한다.
=> 각 노드에 대한 현재까지의 최단 거리의 정보를 항상 1차원 리스트에 저장하며 리스트를 계속 갱신함
=> 매번 현재 처리하고 있는 노드를 기준으로 주변 간선을 확인한다.
* 음의 간선이 없을 때 정상적으로 작동한다.
* 현실 세계에서의 길은 음의 간선으로 표현되지 않으므로 데이크스트라 알고리즘은 실제로 GPS의 기본 알고리즘으로 채택되곤 한다.
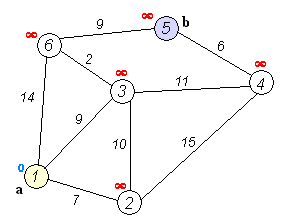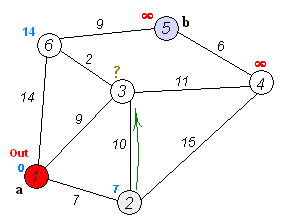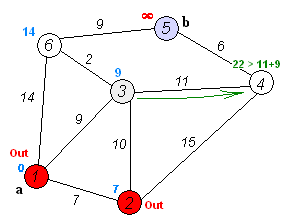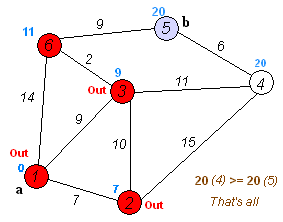
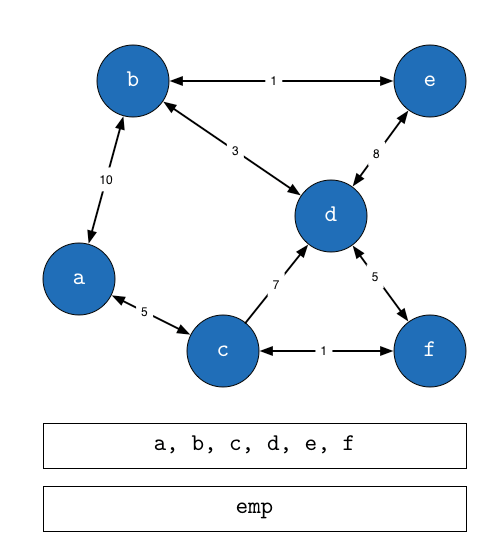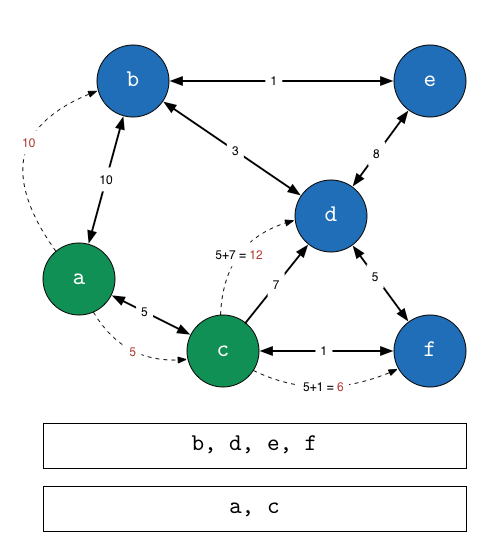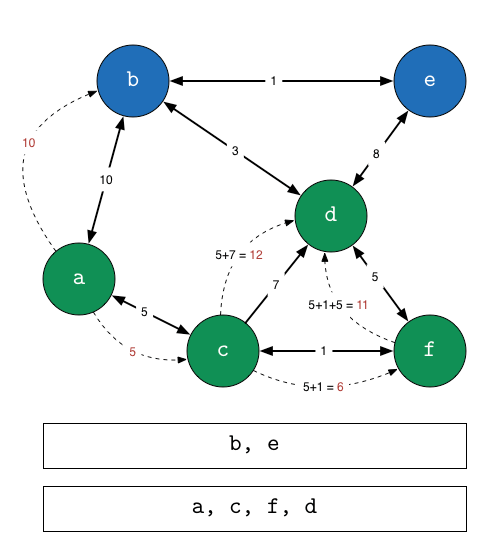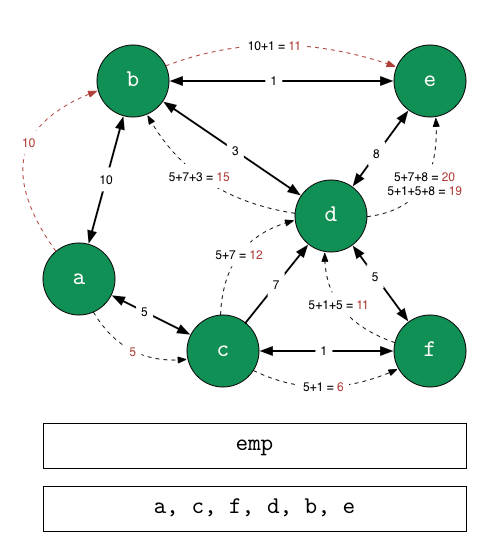
- 출발 노드를 설정한다.
- 출발 노드를 기준으로 각 노드의 최소 비용을 저장한다.
- 방문하지 않은 노드 중에서 가장 적은 비용이 드는 노드를 선택한다.
- 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용의 경로를 갱신한다.
- 3-4번 반복
*소스 코드
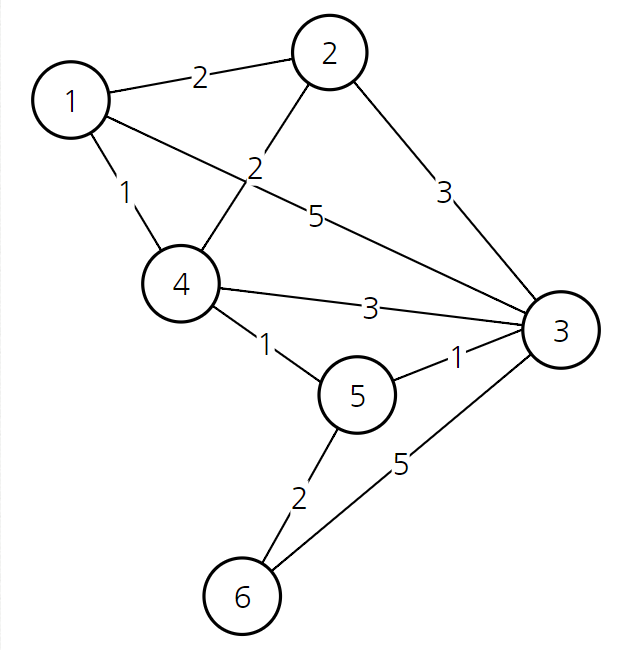
1) 시간복잡도 O(N**2)
// C++
#include <stdio.h>
int number = 6;
int INF = 1000000000;
// 전체 그래프 초기화
int a[6][6] = {
{0, 2, 5, 1, INF, INF},
{2, 0, 3, 2, INF, INF},
{5, 3, 0, 3, 1, 5},
{1, 2, 3, 0, 1, INF},
{INF, INF, 1, 1, 0, 2},
{INF, INF, 5, INF, 2, 0}
};
bool v[6]; // 방문된 노드
int d[6]; // 최단 거리를 저장할 공간
// 최단 거리를 가지는 정점 반환
int getShortestNodesIndex(void) {
int min = INF;
int index = 0;
// 선형탐색
for (int i = 0; i < number; i++) {
if (d[i] < min && !v[i]) {
min = d[i];
index = i;
}
}
return index;
}
// 다익스트라 수행 함수
void dijkstra(int start) {
for (int i = 0; i< number; i++) {
d[i] = a[start][i];
}
v[start] = true;
for (int i = 0; i < number - 2; i++) {
int current = getShortestNodesIndex();
v[current] = true;
for (int j = 0; j < 6; j++) {
if(!v[j]) {
if(d[current] + a[current][j] < d[j]) {
d[j] = d[current] + a[current][j];
}
}
}
}
}
int main(void) {
dijkstra(0);
for (int i = 0; i < number; i++) {
printf("%d ", d[i]);
}
}
# Python
number = 6
INF = int(1e9) # 10억
a = [
[0, 2, 5, 1, INF, INF],
[2, 0, 3, 2, INF, INF],
[5, 3, 0, 3, 1, 5],
[1, 2, 3, 0, 1, INF],
[INF, INF, 1, 1, 0, 2],
[INF, INF, 5, INF, 2, 0]
]
v = [False] * (number)
d = [INF] * (number)
def getShortestNodesIndex():
min = INF
index = 0
for i in range(number):
if d[i] < min and not v[i]:
min = d[i]
index = i
return index
def dijkstra(start):
# 시작 노드에 대해서 초기화
d[start] = 0
v[start] = True
for i in range(number):
d[i] = a[start][i]
# 시작 노드를 제외한 전체 n - 1 개의 노드에 대한 반복
for i in range(number - 2):
current = getShortestNodesIndex()
v[current] = True
for j in range(number):
if not v[j]:
if d[current] + a[current][j] < d[j]:
d[j] = d[current] + a[current][j]
if __name__ == "__main__":
dijkstra(0)
for i in range(number):
print(d[i])
// Javascript
let number = 6;
let INF = 1000000000;
// 전체 그래프 초기화
let a = [
[0, 2, 5, 1, INF, INF],
[2, 0, 3, 2, INF, INF],
[5, 3, 0, 3, 1, 5],
[1, 2, 3, 0, 1, INF],
[INF, INF, 1, 1, 0, 2],
[INF, INF, 5, INF, 2, 0]
];
let v = [false, false, false, false, false, false]; // 방문된 노드
let d = [0, 0, 0, 0, 0, 0]; // 최단 거리를 저장할 공간
// 최단 거리를 가지는 정점 반환
function getShortestNodesIndex() {
let min = INF;
let index = 0;
// 선형탐색
for (let i = 0; i < number; i++) {
if (d[i] < min && !v[i]) {
min = d[i];
index = i;
}
}
return index;
}
// 다익스트라 수행 함수
function dijkstra(start) {
for (let i = 0; i< number; i++) {
d[i] = a[start][i];
}
v[start] = true;
for (let i = 0; i < number - 2; i++) {
let current = getShortestNodesIndex();
v[current] = true;
for (let j = 0; j < 6; j++) {
if(!v[j]) {
if(d[current] + a[current][j] < d[j]) {
d[j] = d[current] + a[current][j];
}
}
}
}
}
function main() {
dijkstra(0);
console.log(d);
}
main();
// Java
public class Main
{
private static int number = 6;
private static int INF = 1000000000;
private static int[][] a = {
{0, 2, 5, 1, INF, INF},
{2, 0, 3, 2, INF, INF},
{5, 3, 0, 3, 1, 5},
{1, 2, 3, 0, 1, INF},
{INF, INF, 1, 1, 0, 2},
{INF, INF, 5, INF, 2, 0}
};
private static boolean[] v = new boolean[6];
private static int[] d = new int[6];
private static int getShortestNodesIndex() {
int min = INF;
int index = 0;
for (int i = 0; i < number; i++) {
if (d[i] < min && !v[i]) {
min = d[i];
index = i;
}
}
return index;
}
private static void dijkstra(int start) {
for (int i = 0; i< number; i++) {
d[i] = a[start][i];
}
v[start] = true;
for (int i = 0; i < number - 2; i++) {
int current = getShortestNodesIndex();
v[current] = true;
for (int j = 0; j < number; j++) {
if(!v[j]) {
if(d[current] + a[current][j] < d[j]) {
d[j] = d[current] + a[current][j];
}
}
}
}
}
public static void main(String[] args) {
dijkstra(0);
for (int i = 0; i < number; i++) {
System.out.printf("%d ", d[i]);
}
}
}
2) Heap을 이용하여 시간복잡도 O(logN)으로 줄이기
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int number = 6;
int INF = 1000000000;
vector<pair<int, int> > a[7]; // 간선 정보
int d[7]; // 최단 거리
void dijkstra(int start) {
d[start] = 0;
priority_queue<pair<int, int> > pq; // heap
pq.push(make_pair(start, 0));
// 가까운 순서대로 처리하므로 큐를 사용
while(!pq.empty()) {
int current = pq.top().first;
// 짧은 것이 먼저 오도록 음수화함
int distance = -pq.top().second;
pq.pop();
// 최단 거리가 아닌 경우 skip
if(d[current] < distance) continue;
for (int i = 0; i < a[current].size(); i++) {
// 선택된 노드의 인접노드
int next = a[current][i].first;
// 선택된 노드를 거쳐서 인접 노드로 가는 비용
int nextDistance = distance + a[current][i].second;
// 기존 최소 비용보다 더 저렴하다면 교차
if (nextDistance < d[next]) {
d[next] = nextDistance;
pq.push(make_pair(next, -nextDistance));
}
}
}
}
int main(void) {
// 기본적으로 연결되지 않은 경우 비용은 무한
for (int i = 1; i <= number; i++) {
d[i] = INF;
}
a[1].push_back(make_pair(2, 2));
a[1].push_back(make_pair(3, 5));
a[1].push_back(make_pair(4, 1));
a[2].push_back(make_pair(1, 2));
a[2].push_back(make_pair(3, 2));
a[2].push_back(make_pair(4, 2));
a[3].push_back(make_pair(1, 5));
a[3].push_back(make_pair(2, 3));
a[3].push_back(make_pair(4, 3));
a[3].push_back(make_pair(5, 1));
a[3].push_back(make_pair(6, 5));
a[4].push_back(make_pair(1, 1));
a[4].push_back(make_pair(2, 2));
a[4].push_back(make_pair(3, 3));
a[4].push_back(make_pair(5, 1));
a[5].push_back(make_pair(3, 1));
a[5].push_back(make_pair(4, 1));
a[5].push_back(make_pair(6, 2));
a[6].push_back(make_pair(3, 5));
a[6].push_back(make_pair(5, 2));
dijkstra(1);
for (int i = 1; i <= number; i++) {
printf("%d ", d[i]);
}
}
# Python
import heapq
number = 6
INF = int(1e9) # 10억
a = [[] for i in range(number + 1)]
d = [INF] * (number + 1)
def dijkstra(start):
# 시작 노드에 대해서 초기화
q = []
d[start] = 0
# 시작 노드로 가기 위한 최단 경로는 0으로 설정하여 큐에 삽입
heapq.heappush(q, (0, start))
while q:
# q가 안 비어있다면 가장 최단 거리 노드 정보 꺼내기
dist, now = heapq.heappop(q)
# 현재 노드가 이미 처리된 적 있다면 무시
if d[now] < dist: continue
for i in a[now]:
# 인접 노드 확인
cost = dist + i[1]
if cost < d[i[0]]:
d[i[0]] = cost
heapq.heappush(q, (cost, i[0]))
if __name__ == "__main__":
a[1].append((2, 2))
a[1].append((3, 5))
a[1].append((4, 1))
a[2].append((1, 2))
a[2].append((3, 2))
a[2].append((4, 2))
a[3].append((1, 5))
a[3].append((2, 3))
a[3].append((4, 3))
a[3].append((5, 1))
a[3].append((6, 5))
a[4].append((1, 1))
a[4].append((2, 2))
a[4].append((3, 3))
a[4].append((5, 1))
a[5].append((3, 1))
a[5].append((4, 1))
a[5].append((6, 2))
a[6].append((3, 5))
a[6].append((5, 2))
dijkstra(1)
for i in range(1, number + 1):
print(d[i])반응형
'Algorithm > 알고리즘 스터디(2021.07)' 카테고리의 다른 글
| [Algorithm] Topology Sort (위상 정렬) (0) | 2021.10.17 |
|---|---|
| [Algorithm] Floyd Warshall Algorithm (플로이드 와샬 알고리즘) (0) | 2021.10.17 |
| [Algorithm] 에라토스테네스의 체 (0) | 2021.10.04 |
| [Algorithm] 다이나믹 프로그래밍 타일링 문제 풀어보기 (2/2) (백준 2133번, 14852번 ) (0) | 2021.09.26 |
| [Algorithm] 다이나믹 프로그래밍 타일링 문제 풀어보기 (1/2) (백준 11726번, 11727번) (0) | 2021.09.26 |





