Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- Python
- 코딩테스트합격자되기
- 항해플러스
- redux-saga
- C++
- 매일메일
- JavaScript
- 알고리즘
- react
- createSlice
- react-redux
- 테코테코
- Get
- java
- redux-toolkit
- 프로그래머스
- json-server
- maeil-mail
- SW
- useDispatch
- axios
- 자바
- react-router
- programmers
- 항해99
- sw expert academy
- 리액트
- 이코테
- Algorithm
- redux
Archives
- Today
- Total
Binary Journey
[프로그래머스] 소수 찾기 본문
반응형
출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges
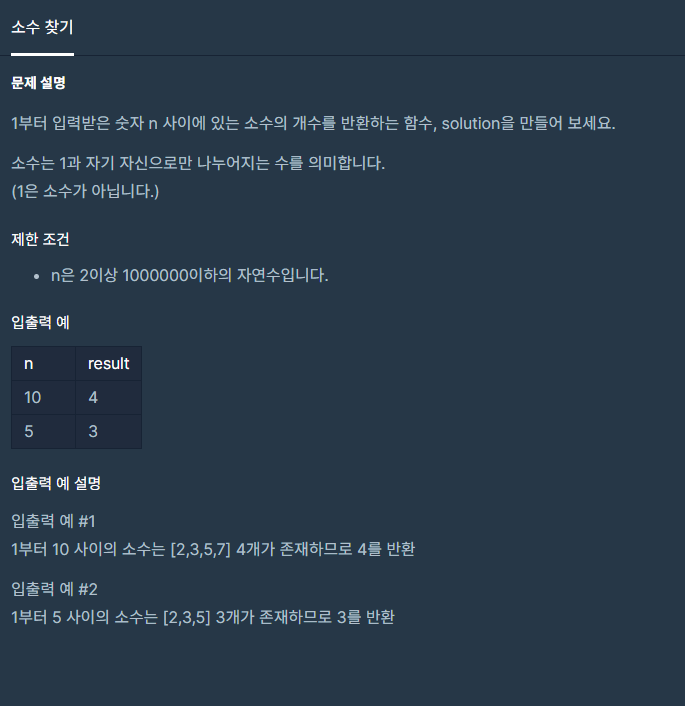
효율성 체크도 있기 때문에 잘 생각해야 한다.
** Javascript
1) 첫 제출 (정확성 테스트는 통과하나 효율성 테스트에서 실패)
function solution(n) {
let count = 0;
for (let i = 2; i <= n; i++) {
if (isPrime(i)) count++;
}
return count;
}
function isPrime(num) {
if(num < 2) return false;
for(let i = 2; i <= Math.floor(Math.sqrt(num)); i++) {
if(num % i == 0) return false;
}
return true;
}
소수구하기 + 시간복잡도로 구글링하여 에라토스테네스의 체를 발견하였다.
2) 정확성 효율성 둘다 통과
function solution(n) {
let pn = new Array(n).fill(1);
pn[0] = 0;
for (let i = 2; i ** 2 <= n; i++) {
if (pn[i - 1]) {
for (let j = i ** 2; j <= n; j+= i) {
pn[j - 1] = 0;
}
}
}
return pn.filter(n => n).length;
}
** Java
import java.util.*;
class Solution {
public int solution(int n) {
int[] pn = new int[n];
Arrays.fill(pn, 1);
pn[0] = 0;
for (int i = 2; (int) Math.pow(i, 2) <= n; i++) {
if(pn[i - 1] == 1) {
for (int j = (int) Math.pow(i, 2); j <= n; j += i) {
pn[j - 1] = 0;
}
}
}
return Arrays.stream(pn).filter(x -> x > 0).toArray().length;
}
}
** Python
def solution(n):
pn = [1] * (n + 1)
for i in range(2, int(n ** 0.5) + 1) :
if pn[i] == 1 :
for j in range(2 * i, n + 1, i) :
pn[j] = 0
return len([x for x in range(2, n + 1) if pn[x] == 1])
* 에라토스테네스의 체
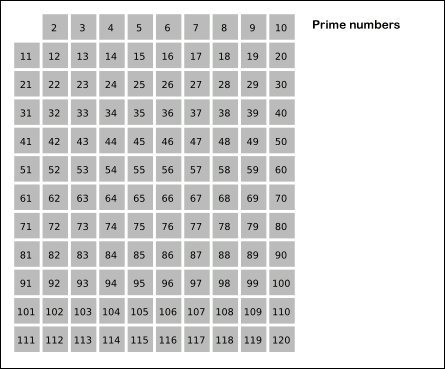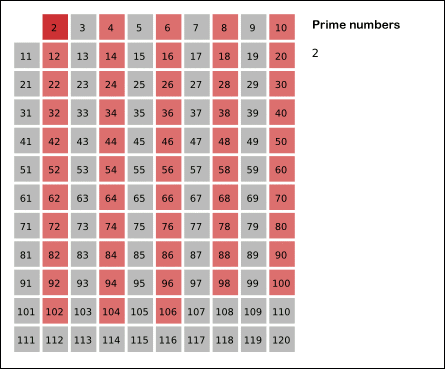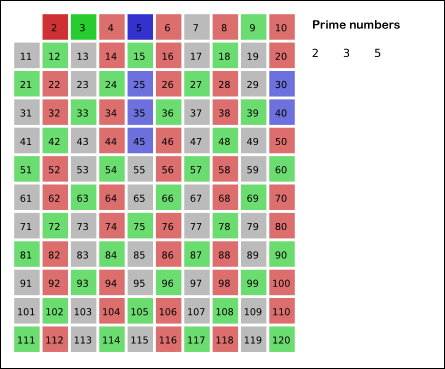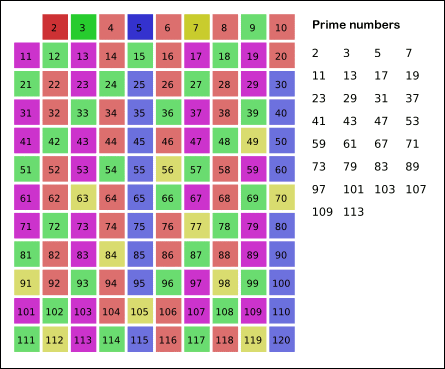
위 그림과 같이 1 - 120 안에 속하는 소수 찾기
1. 11^2 < 120 < 12^2 이므로 자기 자신의 배수를 찾아줘야 할 수는 11까지이다.
2. 2부터 11까지 자기 자신을 제외한 배수를 지운다.
1) Python 구현 예제
def prime_list(n):
# 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
sieve = [True] * n
# n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
m = int(n ** 0.5)
for i in range(2, m + 1):
if sieve[i] == True: # i가 소수인 경우
for j in range(i+i, n, i): # i이후 i의 배수들을 False 판정
sieve[j] = False
# 소수 목록 산출
return [i for i in range(2, n) if sieve[i] == True]
# 출처: https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4
2) C++ 구현 예제
void Eratos(int n)
{
/* 만일 n이 1보다 작거나 같으면 함수 종료 */
if (n <= 1) return;
/* 2부터 n까지 n-1개를 저장할 수 있는 배열 할당
배열 참조 번호와 소수와 일치하도록 배열의 크기는
n+1 길이만큼 할당(인덱스 번호 0과 1은 사용하지 않음) */
bool* PrimeArray = new bool[n + 1];
/* 배열초기화: 처음엔 모두 소수로 보고 true값을 줌 */
for (int i = 2; i <= n; i++)
PrimeArray[i] = true;
/* 에라토스테네스의 체에 맞게 소수를 구함
만일, PrimeArray[i]가 true이면 i 이후의 i 배수는 약수로 i를
가지고 있는 것이 되므로 i 이후의 i 배수에 대해 false값을 준다.
PrimeArray[i]가 false이면 i는 이미 소수가 아니므로 i의 배수 역시
소수가 아니게 된다. 그러므로 검사할 필요도 없다.
또한 i*k (k < i) 까지는 이미 검사되었으므로 j시작 값은 i*2 에서 i*i로 개선할 수 있다.
*/
for (int i = 2; i * i <= n; i++)
{
if (PrimeArray[i])
for (int j = i * i; j <= n; j += i)
PrimeArray[j] = false;
}
// 이후의 작업 ...
}
// 출처: https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4
반응형
'프로그래머스 > level 1' 카테고리의 다른 글
| [프로그래머스][위클리챌린지] 4주차 직업군 추천하기 (0) | 2021.08.30 |
|---|---|
| [프로그래머스] 실패율 (0) | 2021.08.23 |
| [프로그래머스] 서울에서 김서방 찾기 (0) | 2021.08.23 |
| [프로그래머스] 수박수박수박수박수박수? (0) | 2021.08.23 |
| [프로그래머스] 문자열을 정수로 바꾸기 (0) | 2021.08.23 |




