출처: 프로그래머스 코딩 테스트 연습, https://programmers.co.kr/learn/challenges
https://programmers.co.kr/learn/courses/30/lessons/12940
코딩테스트 연습 - 최대공약수와 최소공배수
두 수를 입력받아 두 수의 최대공약수와 최소공배수를 반환하는 함수, solution을 완성해 보세요. 배열의 맨 앞에 최대공약수, 그다음 최소공배수를 넣어 반환하면 됩니다. 예를 들어 두 수 3, 12의
programmers.co.kr

내 풀이는 이렇다.
** Javascript
function greatestCommonDivisor(x, y) {
return y ? greatestCommonDivisor(y, x % y) : x;
}
function leastCommonMultiple(x, y) {
return x * y / greatestCommonDivisor(x, y);
}
function solution(n, m) {
return [greatestCommonDivisor(n, m), leastCommonMultiple(n, m)];
}
다른 사람 풀이 중 진짜로 이게 머선129 외친 풀이를 가져와 봤다.
// 문제가 개편되었습니다. 이로 인해 함수 구성이나 테스트케이스가 변경되어, 과거의 코드는 동작하지 않을 수 있습니다.
// 새로운 함수 구성을 적용하려면 [코드 초기화] 버튼을 누르세요. 단, [코드 초기화] 버튼을 누르면 작성 중인 코드는 사라집니다.
function gcdlcm(a, b) {
var r;
for(var ab= a * b; r = a % b; a = b, b = r){}
return [b, ab / b];
}
** Java
class Solution {
public int[] solution(int n, int m) {
int[] answer = new int[2];
answer[0] = getGCD(n, m);
answer[1] = getLCM(n, m);
return answer;
}
private int getGCD(int x, int y) {
return (y > 0) ? getGCD(y, x % y) : x;
}
private int getLCM(int x, int y) {
return x * y / getGCD(x, y);
}
}
** Python
def getGCD(a, b):
return getGCD(b, a % b) if b > 0 else a
def getLCM(a, b):
return a * b / getGCD(a, b)
def solution(n, m):
return [getGCD(n, m), getLCM(n, m)]
python 의 경우 다른 사람 풀이 중에 참고할 만한 풀이를 가져왔다.
def solution(n, m):
gcd = lambda a,b : b if not a%b else gcd(b, a%b)
lcm = lambda a,b : a*b//gcd(a,b)
return [gcd(n, m), lcm(n, m)]
** 풀이 설명
임의의 두 수의 최소공배수와 최대공약수를 구한다면
어릴 때 대부분 이렇게 구했을 것이다.
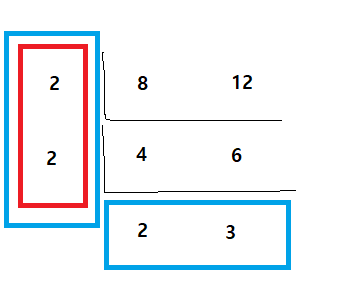
여기서 빨간색 박스 내 숫자들의 곱이 최대공약수이고
파란색 박스 내 숫자들의 곱이 최소공배수가 된다.
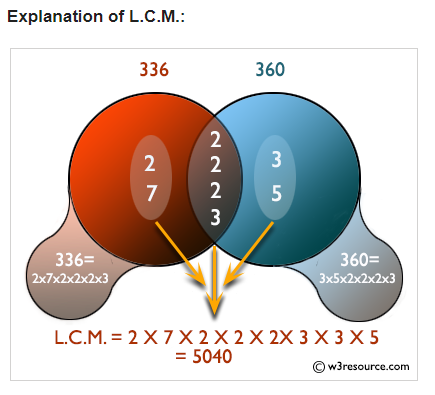
그림으로 쉽게 다시 설명하면 두 수의 합집합이 최소공배수이고 교집합이 최대공약수이다.
만약 덧셈이라면 a,b 합집합 = a 집합 + b 집합 - (a, b 교집합) 이겠지만
제곱근 같이 곱셈의 경우 a,b 합집합 = a 집합 * b 집합 / (a, b 교집합) 이렇게 된다.
따라서 최대공약수를 먼저 구하고 나서 두 수의 곱 / 최대공약수 로 최소공배수를 구하면 된다.
자바스크립트로 알고리즘 정리하기 #6 수학1 (나머지 연산, 최대 공약수)
나머지연산 최대공약수 최소공배수 개념
velog.io
풀이에 달린 댓글들을 보니 유클리드 호제법이 언급되었는데 위 블로그에 유클리드 호제법에 관한 설명도 있다.
내 풀이에서 최대공약수도 유클리드 호제법을 이용한 것이다.
유클리드 호제법의 기본 원리는 a를 b로 나눈 나머지를 r이라고 했을 때, GCD(a, b) = GCD(b, r)과 같다는 것이다.
r이 0이라면, 그 때의 b가 최대공약수이다.
a = 24, b = 16을 가정하면, GCD(24, 16) = GCD(16, 8) = GCD(8, 0)
GCD = 8
GCD(a, b) = GCD(b, a % b)
위 규칙에 따라 함수를 만들면 다음과 같이 된다.
// javascript
let getGCD = (a, b) => (b > 0 ? getGCD(b, a % b) : a);// java
public static int gcd(int p, int q) {
if (q == 0) return p;
return gcd(q, p % q);
}
위키피디에서는 유클리드 호제 최대공약수 알고리즘도 설명해주고 있다.
1. 입력으로 두 수 m,n(m>n)이 들어온다.
2. n이 0이라면, m을 출력하고 알고리즘을 종료한다.
3. m이 n으로 나누어 떨어지면, n을 출력하고 알고리즘을 종료한다.
4. 그렇지 않으면, m을 n으로 나눈 나머지를 새롭게 m에 대입하고, m과 n을 바꾸고 3번으로 돌아온다.
https://ko.wikipedia.org/wiki/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%ED%98%B8%EC%A0%9C%EB%B2%95
유클리드 호제법 - 위키백과, 우리 모두의 백과사전
유클리드 호제법(-互除法, Euclidean algorithm) 또는 유클리드 알고리즘은 2개의 자연수 또는 정식(整式)의 최대공약수를 구하는 알고리즘의 하나이다. 호제법이란 말은 두 수가 서로(互) 상대방 수를
ko.wikipedia.org
'프로그래머스 > level 1' 카테고리의 다른 글
| [프로그래머스] 짝수와 홀수 (0) | 2021.08.03 |
|---|---|
| [프로그래머스] 콜라츠 추측 (0) | 2021.08.03 |
| [프로그래머스] 시저 암호 (0) | 2021.07.27 |
| [프로그래머스] 평균 구하기 (0) | 2021.07.23 |
| [프로그래머스] 하샤드 수 (0) | 2021.07.23 |