| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- json-server
- 리액트
- C++
- 매일메일
- SW
- react
- react-redux
- java
- 코딩테스트합격자되기
- programmers
- 프로그래머스
- axios
- Get
- 이코테
- 자바
- maeil-mail
- redux
- redux-saga
- 항해99
- JavaScript
- 테코테코
- 알고리즘
- createSlice
- Python
- sw expert academy
- 항해플러스
- useDispatch
- react-router
- Algorithm
- redux-toolkit
- Today
- Total
Binary Journey
[Algorithm] 이진 트리의 구현과 순회 알고리즘 본문
알고리즘의 개요와 실습 환경 구축 - 인프런 | 학습 페이지
지식을 나누면 반드시 나에게 돌아옵니다. 인프런을 통해 나의 지식에 가치를 부여하세요....
www.inflearn.com
인프런 알고리즘 강의 20강에 대한 리뷰이다.
이진트리는 비선형 자료구조이고 데이터 탐색 속도 증진을 목적으로 한다.
트리는 배열이나 스택, 큐 등의 자료구조와 달리 데이터를 직관적으로 살펴보기 어렵기 때문에 별도의 순회 알고리즘이 필요하다.
Heap 정렬의 경우 완전 이진 트리를 전제로 한다.
불완전한 이진 트리의 경우 데이터 낭비를 피하기 위하여 포인터가 필요하다.
트리 순회 알고리즘은 트리에 저장된 모든 값을 살펴보고 싶을 때 사용한다.
이진 트리의 순회 방법 중 전위 순회(Pre-order Traversal), 중위 순회(In-order Traversal), 후위 순회(Post-order Traversal)가 있으며 이 순회 방법을 통틀어 깊이 우선 순회 방법(Depth First Traversal, DFS)라고 한다.
* 너비 우선 순회 방법(Breadth First Traversal)로는 레벨 순회가 있다.
참고: http://ejklike.github.io/2018/01/09/traversing-a-binary-tree-2.html
Eunji Kim @ CAU - 파이썬을 사용한 이진 트리와 순회 알고리즘 구현 (2)
이전 포스트에서는 이진 탐색 트리 (binary search tree)를 구현해보았다. 트리는 배열이나 스택, 큐 등의 자료구조와 달리 데이터를 직관적으로 살펴보기 어렵다. 따라서 트리를 위한 별도의 순회 알
ejklike.github.io
1. 전위 순회
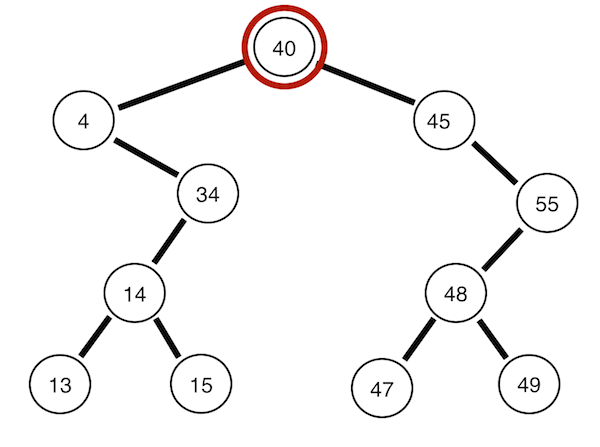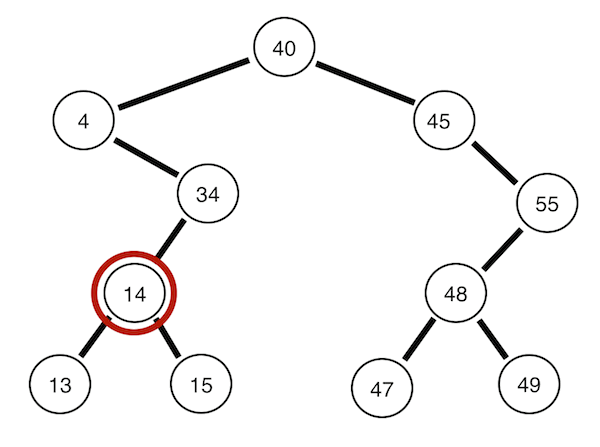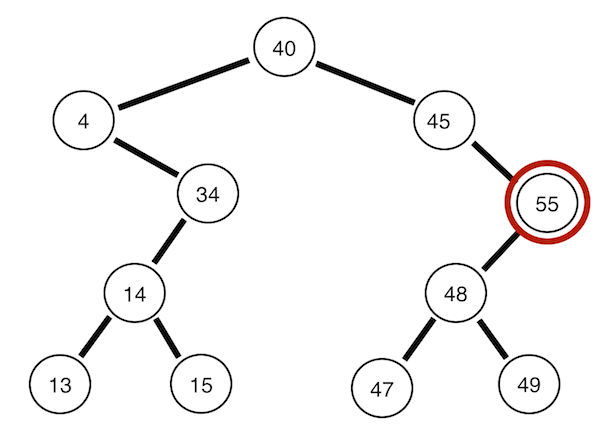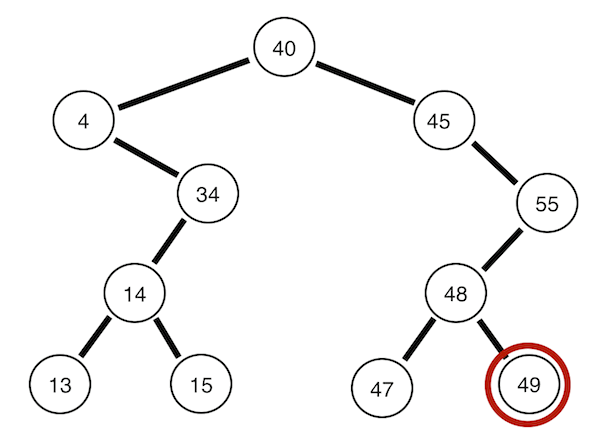
자기 자신(부모 노드) -> 왼쪽 자식 -> 오른쪽 자식
2. 중위 순회
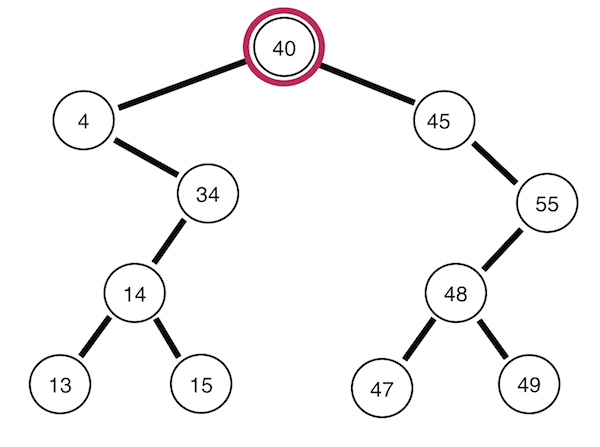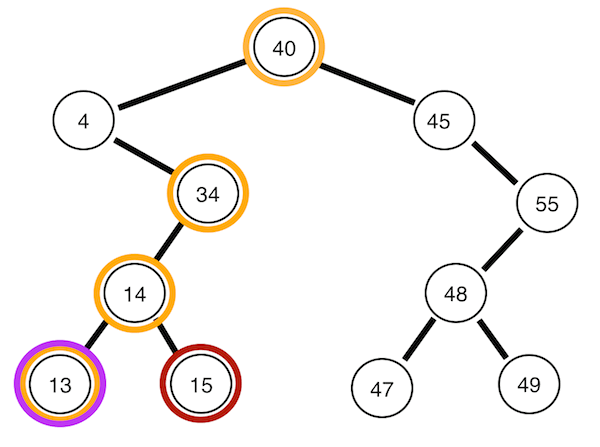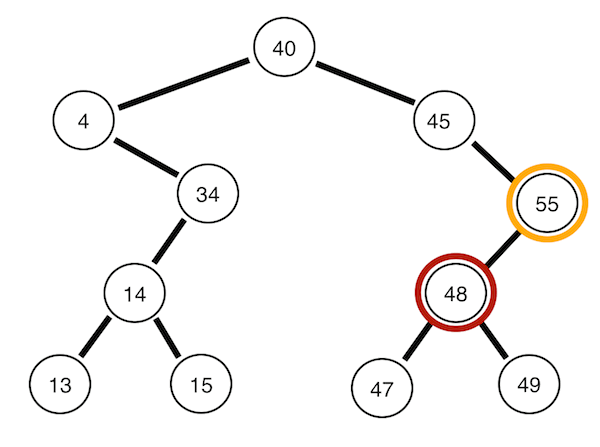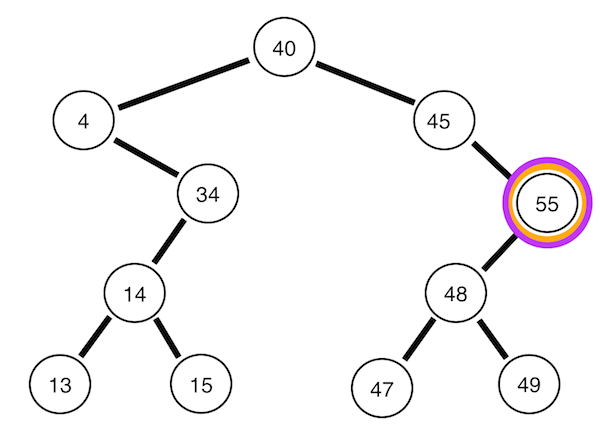
왼쪽 자식 -> 자기 자신 -> 오른쪽 자식
위 이미지를 가져온 블로그에 따르면 이진 탐색 트리를 정순회하면 정렬된 데이터를 얻을 수 있다는데 무슨 말인지 모르겠다.
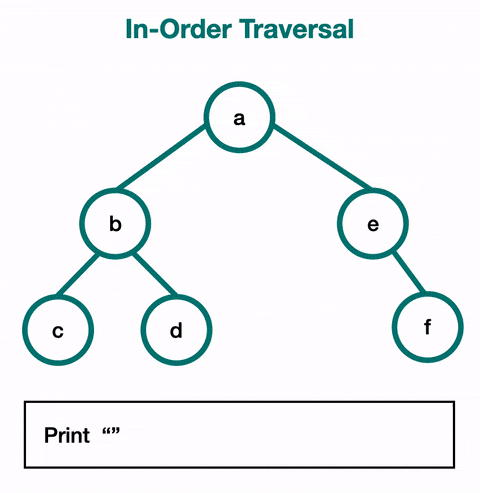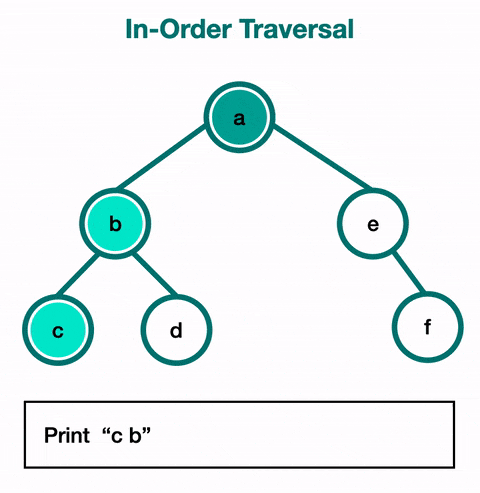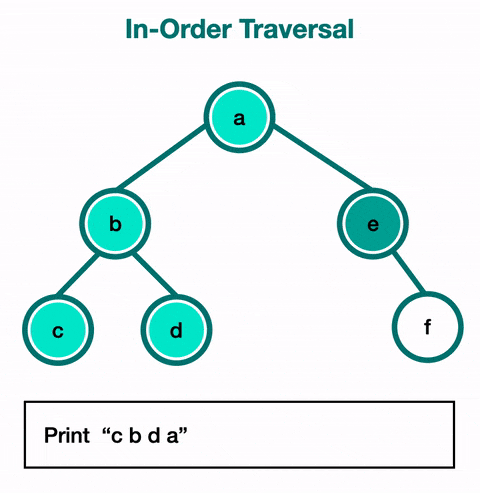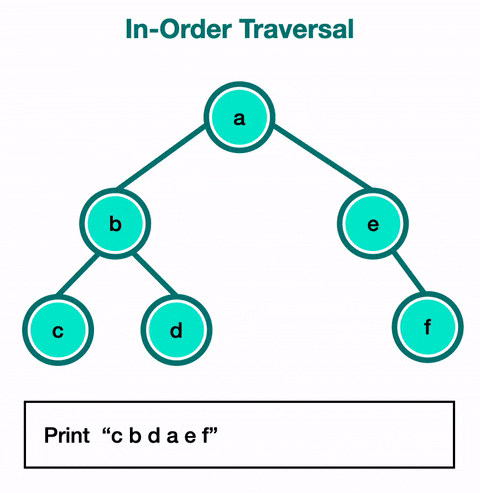
위 이미지를 보면 이해할 것 같기도 하다.
3. 후위 순회
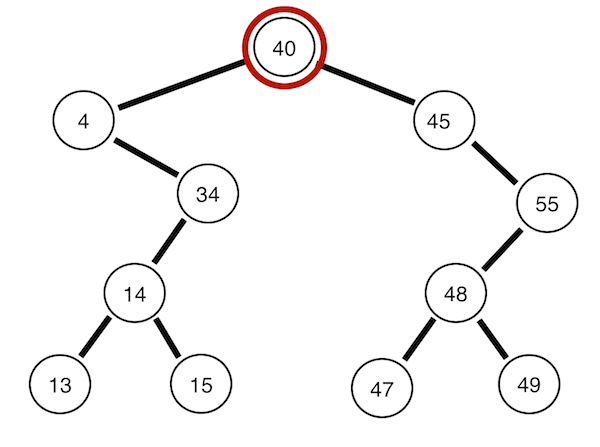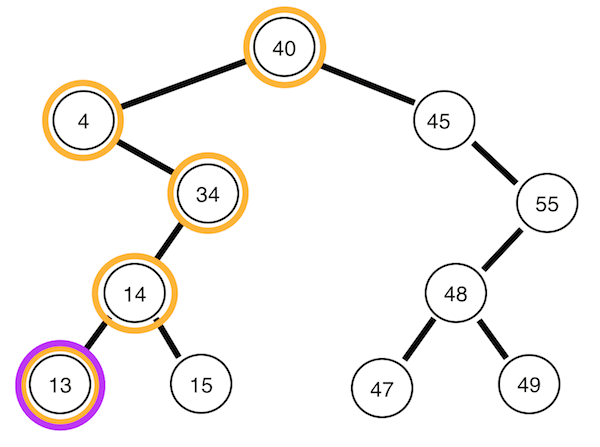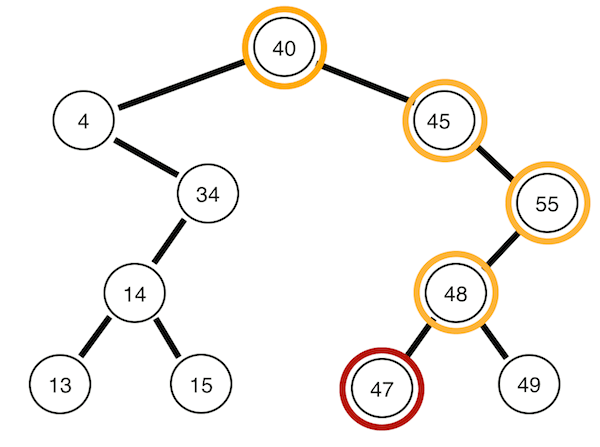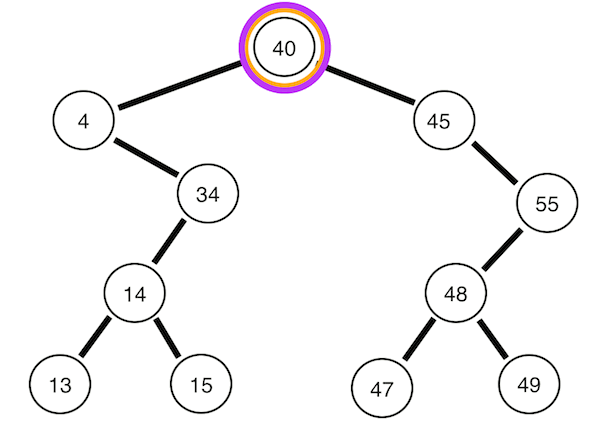
왼쪽 자식 -> 오른쪽 자식 -> 자기 자신
계산 관련 프로그램에서 많이 사용된다.
** C++
#include <iostream>
using namespace std;
int number = 15;
// 하나의 노드 정보를 선언합니다.
typedef struct node *treePointer; // node라는 구조체를 treePointer 라는 이름으로 이용하겠다.
typedef struct node {
int data;
treePointer leftChild, rightChild;
} node;
// 전위 순위 (Pre-order)
void preorder(treePointer ptr) {
if(ptr) {
cout << ptr->data << ' ';
preorder(ptr->leftChild);
preorder(ptr->rightChild);
}
}
// 중위 순위 (In-order)
void inorder(treePointer ptr) {
if(ptr) {
inorder(ptr->leftChild);
cout << ptr->data << ' ';
inorder(ptr->rightChild);
}
}
// 후위 순위 (Post-order)
void postorder(treePointer ptr) {
if(ptr) {
postorder(ptr->leftChild);
postorder(ptr->rightChild);
cout << ptr->data << ' ';
}
}
int main(void) {
node nodes[number + 1];
for (int i = 1; i <= number; i++) {
nodes[i].data = i;
nodes[i].leftChild = NULL;
nodes[i].rightChild = NULL;
}
for (int i = 1; i <= number; i++) {
if (i % 2 == 0) {
nodes[i / 2].leftChild = &nodes[i];
} else {
nodes[i / 2].rightChild = &nodes[i];
}
}
// preorder(&nodes[1]);
// inorder(&nodes[1]);
postorder(&nodes[1]);
return 0;
}
** Python
(시도중)
class Node(object):
def __init__(self):
self.data = data
self.left = None
self.right = None
if __name__ == "__main__":
nodes = [Node(i) for i in range(1, 16)]
어마어마한 코드를 발견해서 따라서 해봤는데 In-order 에서 자꾸 안된다.
일단 정렬된 트리라서 그런 것 같기도..
class Node(object):
# 이진 탐색 트리를 구현하려면 Node 클래스 정의 필요
# Node 클래스는 노드값(data) 과 좌/우 노드(left/right) 총 세개의 속성이 필요
# 초기화할 때는 데이터 값만 주어지고 좌/우 노드 빈 상태
def __init__(self, data):
self.data = data
self.left = self.right = None
class BinarySearchTree(object):
def __init__(self):
# 빈 트리
self.root = None
# 삽입: 새로운 원소 추가
def insert(self, data):
self.root = self._insert_value(self.root, data)
return self.root is not None
def _insert_value(self, node, data):
if node is None:
node = Node(data)
else:
"""
재귀 사용
새로 추가할 원소의 값을 현재 노드의 값과
비교하여 왼쪽/오른쪽 중 알맞은 위치로
노드를 옮겨가며 삽입 위치 체크
"""
if data <= node.data:
node.left = self._insert_value(node.left, data)
else:
node.right = self._insert_value(node.right, data)
return node
# 탐색: 원하는 값의 존재 유무 확인
def find(self, key):
return self._find_value(self.root, key)
# 재귀를 이용하여 대소관계 비교
def _find_value(self, root, key):
if root is None or root.data == key:
return root is not None
elif key < root.data:
return self._find_value(root.left, key)
else:
return self._find_value(root.right, key)
# 삭제
def delete(self, key):
self.root, deleted = self._delete_value(self.root, key)
return deleted
def _delete_value(self, node, key):
if node is None:
return node, False
deleted = False
if key == node.data:
deleted = True
if node.left and node.right:
# replace the node to the leftmost of node.right
"""
왼쪽 서브 트리와 오른쪽 서브 트리를
각각 A, B라고 할 때, B에서 가장 왼쪽
아래에 위치한 자손을 가져온다.
이 원소는 A의 모든 원소들보다 크면서,
B의 나머지 원소보다 작다
"""
parent, child = node, node.right
while child.left is not None:
parent, child = child, child.left
child.left = node.left
if parent != node:
parent.left = child.right
child.right = node.right
node = child
elif node.left or node.right:
node = node.left or node.right
else:
node = None
elif key < node.data:
node.left, deleted = self._delete_value(node.left, key)
else:
node.right, deleted = self._delete_value(node.right, key)
return node, deleted
def pre_order_traversal(self):
def _pre_order_traversal(root):
if root is None:
pass
else:
print(root.data)
_pre_order_traversal(root.left)
_pre_order_traversal(root.right)
_pre_order_traversal(self.root)
# 자기자신(부모) -> 왼쪽 자식 -> 오른쪽 자식
def in_order_traversal(self):
def _in_order_traversal(root):
if root is None:
pass
else:
_in_order_traversal(root.left)
print(root.data)
_in_order_traversal(root.right)
_in_order_traversal(self.root)
# 왼쪽 자식 -> 자기 자신(부모) -> 오른쪽 자식
def post_order_traversal(self):
def _post_order_traversal(root):
if root is None:
pass
else:
_post_order_traversal(root.left)
_post_order_traversal(root.right)
print(root.data)
_post_order_traversal(self.root)
# 왼쪽 자식 -> 오른쪽 자식 -> 자기자신(부모)
def main() :
array = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11, 12, 13, 14, 15]
bst = BinarySearchTree()
for x in array:
bst.insert(x)
# depth first
bst.pre_order_traversal()
# bst.in_order_traversal()
# bst.post_order_traversal()
if __name__ == "__main__":
# execute only if run as a script
main()출처: http://ejklike.github.io/2018/01/09/traversing-a-binary-tree-2.html
위 버전을 그나마 축약 시킨 버전은 아래와 같다
근데 이것도 원하는 결과는 안 나온다.
class Node:
# 이진 탐색 트리를 구현하려면 Node 클래스 정의 필요
# Node 클래스는 노드값(data) 과 좌/우 노드(left/right) 총 세개의 속성이 필요
# 초기화할 때는 데이터 값만 주어지고 좌/우 노드 빈 상태
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# insert
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the Tree
def PrintTree(self):
if self.left:
self.left.PrintTree()
print(self.data),
if self.right:
self.right.PrintTree()
# Preorder traversal
# Root -> Left ->Right
# 자기자신(부모) -> 왼쪽 자식 -> 오른쪽 자식
def PreorderTraversal(self, root):
result = []
if root:
result.append(root.data)
result = result + self.PreorderTraversal(root.left)
result = result + self.PreorderTraversal(root.right)
return result
# Inorder traversal
# Left -> Root -> Right
# 왼쪽 자식 -> 자기 자신(부모) -> 오른쪽 자식
def inorderTraversal(self, root):
result = []
if root:
result = self.inorderTraversal(root.left)
result.append(root.data)
result = result + self.inorderTraversal(root.right)
return result
# Postorder traversal
# Left ->Right -> Root
# 왼쪽 자식 -> 오른쪽 자식 -> 자기자신(부모)
def PostorderTraversal(self, root):
result = []
if root:
result = self.PostorderTraversal(root.left)
result = result + self.PostorderTraversal(root.right)
result.append(root.data)
return result
def main() :
array = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11, 12, 13, 14, 15]
root = Node(1)
root.insert(2)
root.insert(3)
root.insert(4)
root.insert(5)
root.insert(6)
root.insert(7)
root.insert(8)
root.insert(9)
root.insert(10)
root.insert(11)
root.insert(12)
root.insert(13)
root.insert(14)
root.insert(15)
# print(root.PreorderTraversal(root))
print(root.inorderTraversal(root))
# print(root.PostorderTraversal(root))
if __name__ == "__main__":
# execute only if run as a script
main()
이것도 중위 순위........
# 노드 만들기
# A(val)
# / \
# B(left) C(right)
class Node:
def __init__(self, item):
self.val = item
self.left = None
self.right = None
# 이진트리 만들기
class BinaryTree:
# 초기값 head는 None
def __init__(self):
self.head = Node(None)
self.preorder_list=[]
self.inorder_list=[]
self.postorder_list=[]
# 값 추가하기 head가 없을 경우
def add(self, item):
if self.head.val is None:
self.head.val = item
# head가 있으면 왼쪽배치 or 오른쪽배치
else:
self.__add_node(self.head, item)
# head가 있는 경우
def __add_node(self, cur, item):
print('부모:', cur.val, '자식:', item)
# head 값이 크면 왼쪽으로
if cur.val >= item:
if cur.left is not None:
self.__add_node(cur.left, item)
else:
cur.left = Node(item)
# head 값이 작으면 오른쪽으로
else:
if cur.right is not None:
self.__add_node(cur.right, item)
else:
cur.right = Node(item)
# 찾기!!
def search(self, item):
if self.head.val is None:
return False
else:
return self.__search_node(self.head, item)
def __search_node(self, cur, item):
print(cur.val, item)
if cur.val == item:
return True
else:
if cur.val >= item:
if cur.left is not None:
return self.__search_node(cur.left, item)
else:
return False
else:
if cur.right is not None:
return self.__search_node(cur.right, item)
else:
return False
# 전위순회
def preorder_traverse(self):
if self.head is not None:
self.__preorder(self.head)
def __preorder(self, cur):
self.preorder_list.append(cur.val)
print(cur.val)
if cur.left is not None:
self.__preorder(cur.left)
if cur.right is not None:
self.__preorder(cur.right)
# 중위순회
def inorder_traverse(self):
if self.head is not None:
self.__inorder(self.head)
def __inorder(self, cur):
if cur.left is not None:
self.__inorder(cur.left)
self.inorder_list.append(cur.val)
print(cur.val)
if cur.right is not None:
self.__inorder(cur.right)
# 후위순회
def postorder_traverse(self):
if self.head is not None:
self.__postorder(self.head)
def __postorder(self, cur):
if cur.left is not None:
self.__postorder(cur.left)
if cur.right is not None:
self.__postorder(cur.right)
self.postorder_list.append(cur.val)
print(cur.val)
lst = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
bt = BinaryTree()
for num in lst:
bt.add(num)
# print(bt.search(60))
# 전우
bt.preorder_traverse()
print(bt.preorder_list)
# 중위
bt.inorder_traverse()
print(bt.inorder_list)
# 후위
bt.postorder_traverse()
print(bt.postorder_list)'Algorithm > 알고리즘 스터디(2021.07)' 카테고리의 다른 글
| [Algorithm] 다이나믹 프로그래밍 타일링 문제 풀어보기 (1/2) (백준 11726번, 11727번) (0) | 2021.09.26 |
|---|---|
| [Algorithm] 다이나믹 프로그래밍 (0) | 2021.09.26 |
| [Algorithm] Kruskal Algorithm (크루스칼 알고리즘) (0) | 2021.09.12 |
| [Algorithm] Union-Find (합집합 찾기) (0) | 2021.09.12 |
| [Algorithm] DFS (깊이 우선 탐색) (0) | 2021.09.02 |




